6.1. Poliedros y cuerpos redondos

Ahora te presentamos los cuerpos geométricos más corrientes:

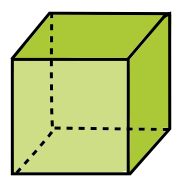
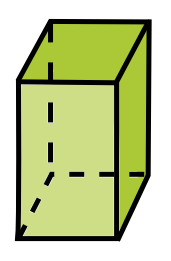
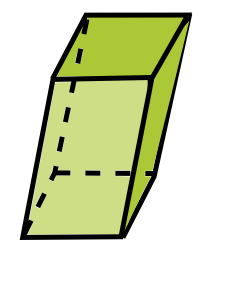
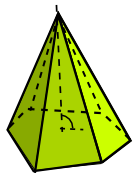
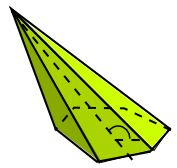
cubo	prisma recto	prisma oblicuo	pirámide recta	pirámide oblicua
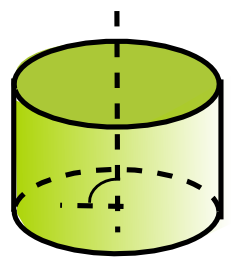
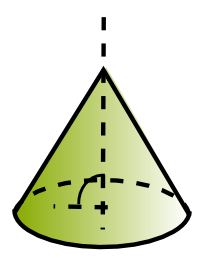
cilindro recto	cilindro oblicuo	cono recto	cono oblicuo	esfera

Observa que los hemos agrupado en dos filas. En general, los elementos de estos cuerpos geométricos se nombran igual que en el cubo.

• Los de la primera fila, tienen en común el tener sus caras poligonales. Cada uno de estos cuerpos recibe el nombre de poliedro. Los tres primeros poliedros se llaman prismas y los restantes, pirámides.

Los de la segunda fila se caracterizan por tener sus bases circulares. Cada uno de estos cuerpos se llama cuerpo redondo o cuerpo de revolución. Los dos primeros son cilindros, los dos siguientes son conos y el último es una esfera. En la figura de la derecha puedes observar que el cono ahí representado se obtiene al hacer girar un triángulo equilátero  alrededor de su altura.

Los elementos de un poliedro son los vértices, las aristas y las caras. Las caras son los polígonos que forman el poliedro. Un vértice es un punto en el que se encuentran los vértices de varias caras. Las aristas son los segmentos comunes a dos caras del poliedro.  

Además de los anteriores elementos mencionados, tenemos:

• ángulo superficial o plano, que es el  que forman dos aristas de una cara que pasen por el mismo vértice,
• ángulo diedro, que es el formado por dos caras que tengan un lado en común.
• ángulo poliedro, que es el formado por todas las caras que tengan un vértice común (la suma de los ángulos internos, en el vértice común, de las caras que forman el ángulo poliedro es menor que 360º.

Los poliedros convexos se clasifican a su vez en dos grandes grupos:

• los regulares, si sus caras son polígonos regulares iguales, también son iguales sus ángulos diedros y sus ángulos poliedros
• los irregulares, son los restantes poliedros

Los poliedros reciben el nombre según el números de caras, así tenemos los tetraedros (cuatro caras), los pentaedros (cinco caras), los exaedros (seis caras), los heptaedros (siete caras), los octaedros (ocho caras) , ..., 

En el enlace http://www.korthalsaltes.com/es/index_n-faces_polyhedron.php puedes encontrar una lista de los nombres de muchos poliedros.