3.2. Posiciones relativas entre puntos, rectas y planos
Las posibles situaciones son:
| - Dos puntos P y Q | |||
| son distintos | Son idénticos. | ||
|
determinan una recta
|
En este caso se dice que son coincidentes
|
||
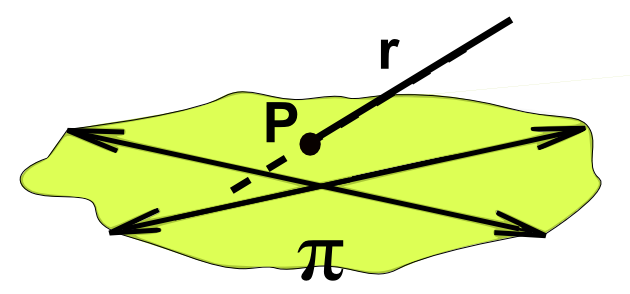
| - un punto P y una recta r | ||||
| El punto está en la recta | el punto no está en la recta
Se dice que el punto es exterior a la recta
|
|||
|
Se dice que el punto pertenece a la recta
|
||||
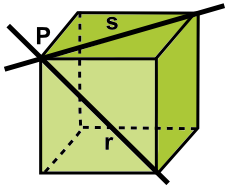
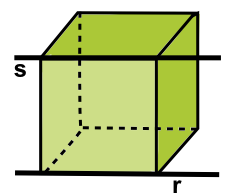
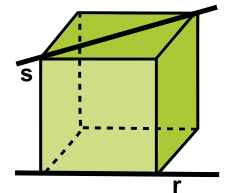
| - Dos rectas r y s | ||||
| (usaremos un cubo como modelo para representarlas) | ||||
|
Tienen un punto en común.
Las rectas son secantes o incidentes.
|
No tienen ningún punto en común, pero están contenidas en el mismo plano.
Las rectas son paralelas no coincidentes o simplemente paralelas.
|
|
No tienen puntos en común y no existe ningún plano que las contenga simultáneamente.
Las rectas se cruzan |
|
|
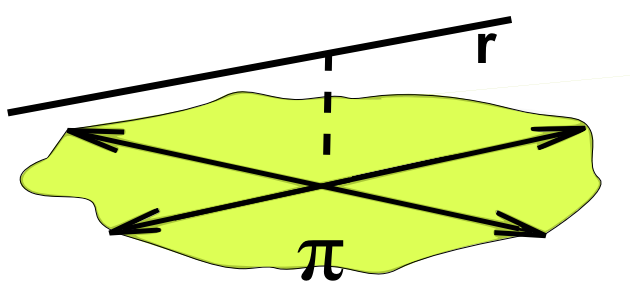
- Una recta y un plano |
||||
|
La recta r atraviesa al plano π por el punto P
La recta es incidente con el plano π y el punto P es el punto de intersección de ambos. El plano y la recta son secantes.
|
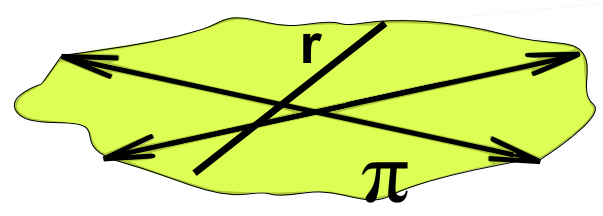
La recta r no tiene puntos en común con el plano π
La recta r y el plano π son paralelos
|
La recta r tiene todos sus puntos en común con el plano π
la recta r está contenida en el plano π
|
||
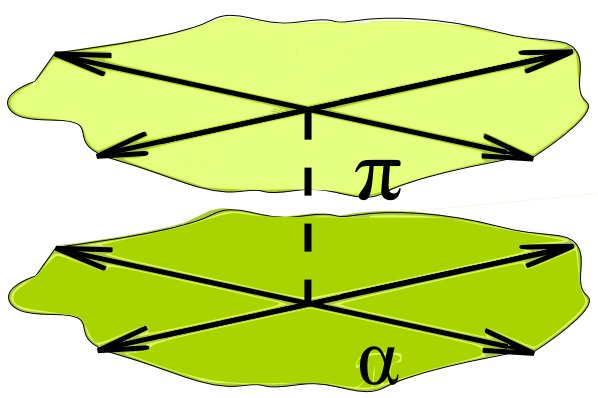
| - Dos planos | ||||
|
Los planos α y π no tienen puntos en común los planos son paralelos no coincidentes o, simplemente, paralelos
|
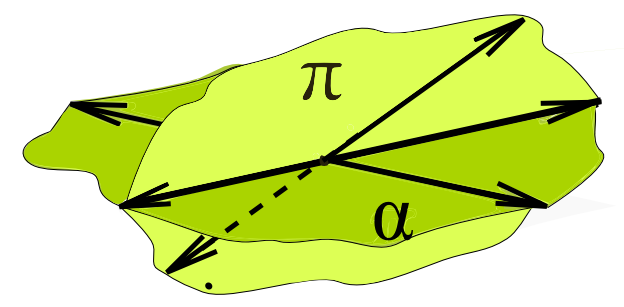
Los planos α y π tienen infinidad de puntos en común, se cortan en una recta r
son planos incidentes o secantes.
|
|||
Obra colocada bajo licencia Creative Commons Attribution Share Alike 3.0 License